许多顶尖大学虽然没明说，但都更喜欢工程、物理、计算机科学和经济学等课程的学生拿到数学A*。能学好Alevel数学，被视为学生可以分析和解决复杂问题能力的证明。
我们今天的主题就探讨：普通学生怎么在Alevel数学中获得A*？
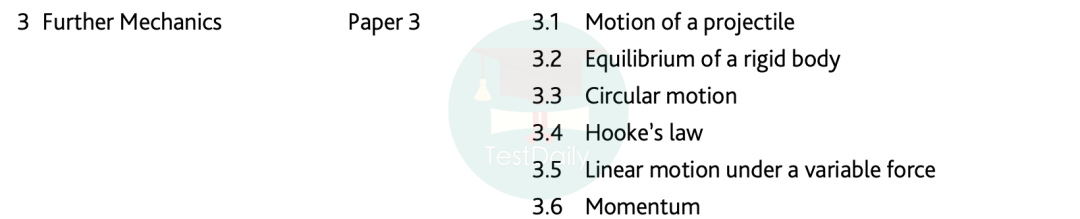
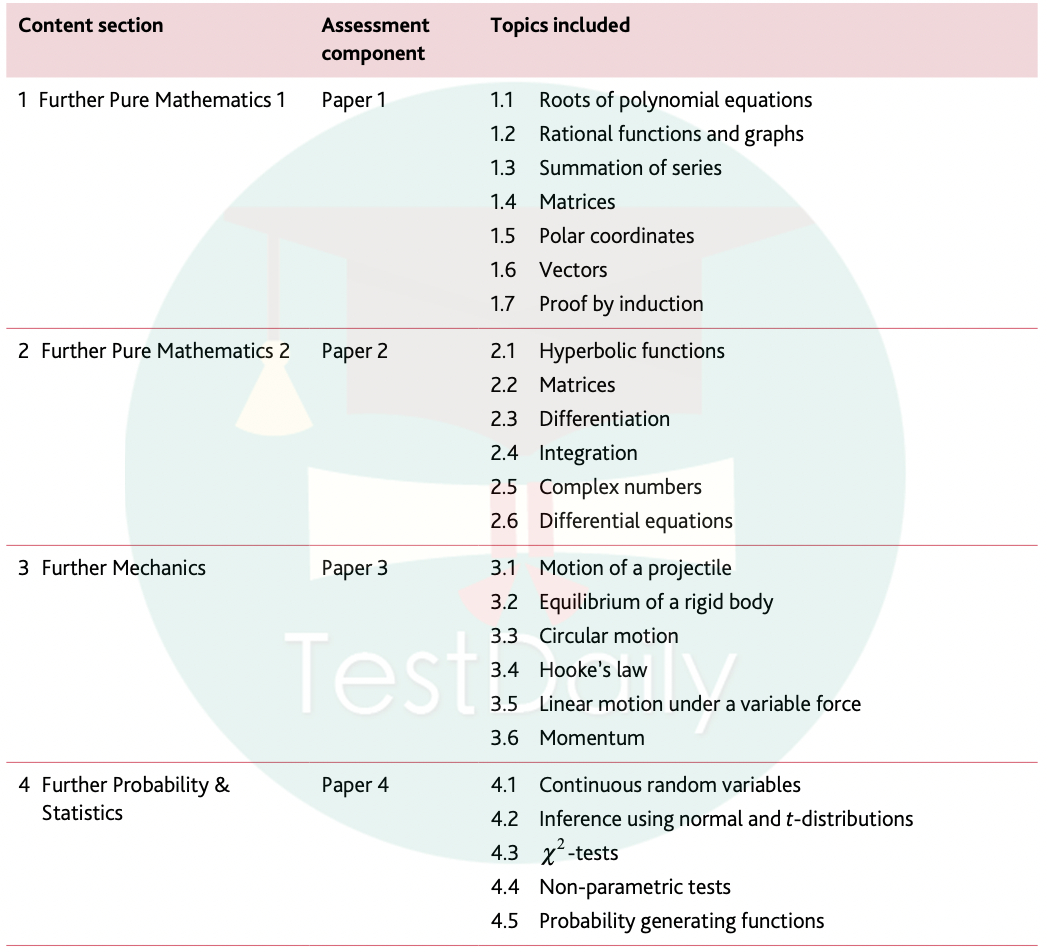
首先我们先来了解一下进阶数学。进阶数学一共分为4个paper，包括Further Pure Mathematics1, Further Pure Mathematics2, Further Mechanics, Further Probability & Statistics。
在AS阶段，学生可以根据自己学校的要求选择FP1和进阶统计，或者FP1和进阶力学进行学习；在AL阶段，我们就可以学习另外两门paper啦。通常学校会建议在AS阶段学习统计，统计相对比力学要更好上手，计算复杂度更小。
图片源于CAIE官方大纲
那么每个Paper怎么考呢？FP1和FP2的卷面分数均为75分, 考生要求在2h内回答完成十余道大题。Further Mechanics和Further Statistics为50分，答题时间1.5h。
根据官方Syllabus，FP1覆盖了关于多项式，数列，矩阵，极坐标，向量以及数学归纳法，而FP2重点则学习双曲方程，复数和微分方程，同时拓展并深入了微积分和矩阵。很多同学好奇：FP1和2的难度是不是差距特别大啊？
小编认为，在知识点上FP2的确需要更“深厚”的微积分能力，而且在解决像微分方程，复数等问题的时候需要的步骤和理解更加繁琐。但是FP1和FP2大部分的知识点并没有重合，因此虽然计算难度和理解难度大了一点，并不会存在像“同是解二次方程，突然从2x+7=y变成了超级复杂的行程问题”的落差。
statistics则更重视“方法论”，根据不一样的情况，我们会学习不同的hypothesis tests。mechanics更加灵活，简单来说是把物理的力学问题模型化，研究一些像平衡，圆周运动，撞击等问题。总之，FM学的还是相当的多，相当的灵活！
拿捏考试第二步：
行军大局的general tips
接下来要说的tips适用于FurtherPure和Statistics。先说FM考试的特点，我觉得总体很“套路化”和“公式化”。“套路化”是学习的每个知识点只有相对应的几种考法，并且每次考试的题型统一。大家可以做好FM一共学了几个章节卷子就会出几道题的准备：一个章节的知识点对应着一道题。
举个例子吧，在FP2学习matrix的时候，我们学习了Eigenvector和Eigenvalue的求法，那考试对应的就是直接问如何从一个已知的3*3矩阵中求这两个，学到的知识点都会以最直接的形式考你！
“公式化”则是在考场的时候更加注重如何去解而不是为什么。比如，在integration章节我们涉及了极坐标下的各种图形的面积和翻转体积，考试的时候会直接让我们利用公式解题而不强调推导过程。同学们听了肯定觉得：这不易如反掌了！
根据这两个总体的特点，我认为唯二的应对策略就是重视学习基础+多刷题多总结。下面我总结了学习的几个step：
如果是跟着学校学，课堂永远放在number1！如果是自学，课本永远是最靠谱的！我的学校老师讲解是完全按照课本逻辑的，比如说，在FP1的polar极坐标中分为3个小节，分别是认识polar coordinate，画图，以及算面积。实际上，最后的FP1考试中极坐标也会只考察这三个知识点。
所以我一直秉承着教材为本的逻辑，考生可以很明确的知道每个章节要掌握的内容。对于市面上的各种notes我一直持有怀疑态度，建议初学者谨慎使用。
还以Polar这章为例，我们都清楚以下当之无愧归属于笔记（教我们如何做Polar和Cartesian的方程转换）
图片为小编整理笔记
那做题呢？几乎每一个知识点下面都对应着examples和solutions。这也就无形中教我们如何把上面记的一大串文字转化成考试可以利用的“方法论”。这部分“方法论”也应该记在笔记中，作为做题的指导方针。
图片为小编整理笔记
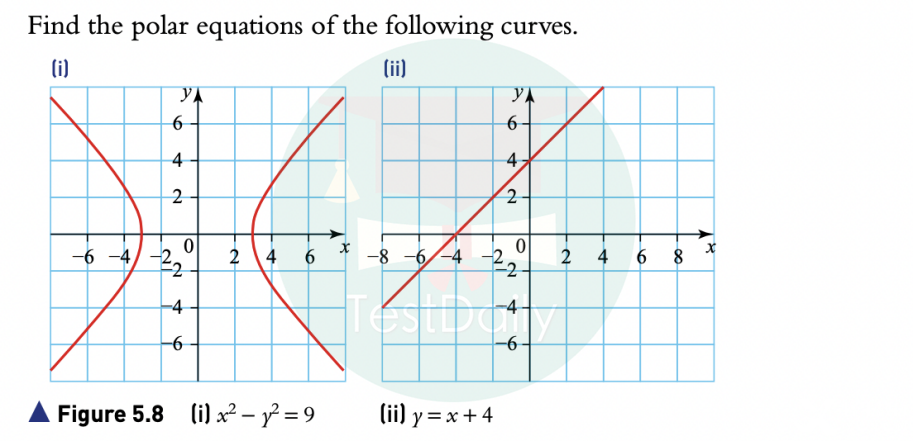
在做完worked example之后，建议大家直接从真题里找题。比如说以May/June 2023的FP1为例子，就像我之前说的，只会有1-2道题出现polar的知识点，所以很容易提取出chapter questions。
我们会发现，sketch的题不就对应着书中的5.2-sketching curve with polar coordinates, area的题就对应着5.3。这种很直接的1V1对应让我们可以点对点的检验知识点是否学习完善。比如，在学完sketch做完worked example之后，就可以去模仿学习过的方法论去挑战真题了。
图片为CAIE May/June 2023FP1真题
当然，尤其对于自学的同学们，如果大家有时间可以整理一个自己的习题册。比如说在学完polar的第三部分area之后，我们在past paper中提取出来很多有关此的题目放到合集中，就像这样。久而久之，你就会收获自己整理的一套chapter questions！
在学完每一个chapter之后都要复习！就以matrix来说吧，你要知道行列式，inverse等等应该怎么求，小的知识点非常繁琐。所以我还是建议同学们用最直接的思维导图的方式捋清楚知识点之间的关系。
如果在学完一个chapter之后整理出这样的一份思维导图和上面提到的worksheet，那么在最终大考复习的时候，要解决的就是根据思维导图的分支去对应相应的worksheet，这不分分钟有了复习攻略。
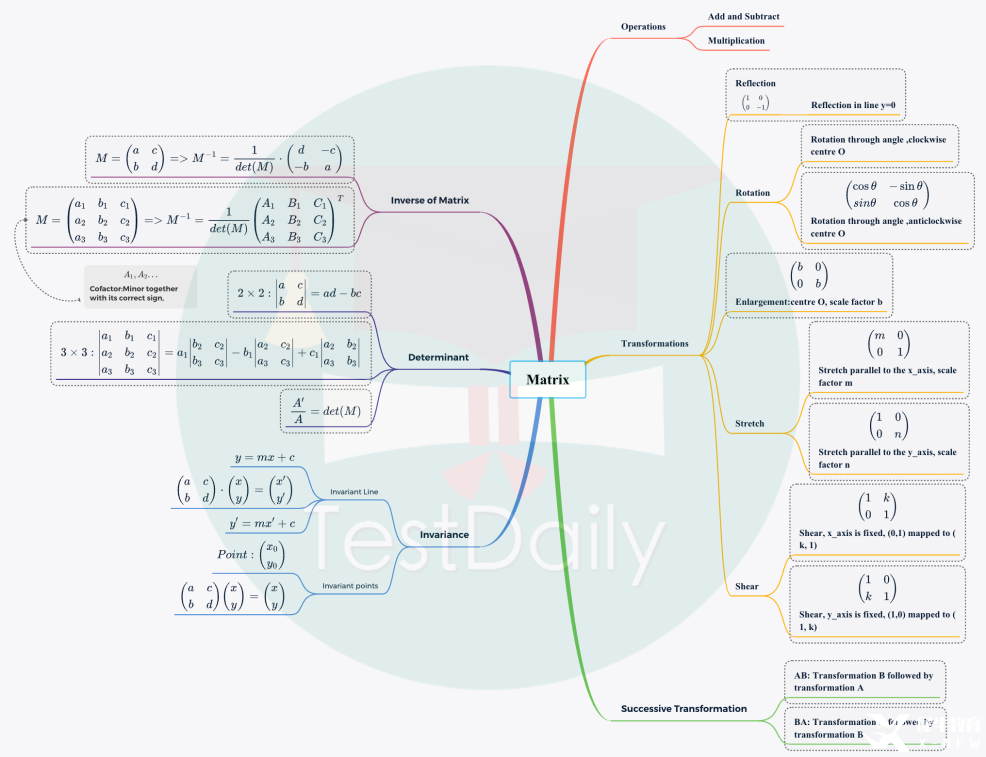图片为小编整理笔记
当然，说完高数非常可控的部分，再说说它让人“恨”的部分——知识点多而且碎；对于初学者解决问题的步骤繁杂，不好入手；积分部分计算量太大。
知识点多和碎倒是恰恰好可以用思维导图的方法解决。步骤繁杂不好入手属further statistics体现的最明显，就以further stats中的Non-parametric tests为例，里面我们学习了Wilcoxon signed-rank test，the Wilcoxon rank-sum test，其中又分为paired-sample sign test，Wilcoxon matched-pairs signed-rank test等等，捋清楚什么样的情况用什么test倒是可以用思维导图解决，那具体的步骤呢？
我的建议是运用“照猫画虎”的方法。比如，你可以先找到一个标准的用Wilcoxon matched-pairs signed-rank test的题目和答案，再在past paper中利用matched-pairs关键词找一道真题。学着solution的方法，一步一步应用到自己的题目中。
不光Further statistics中可以这样，再比如FP2中的微分方程，second order的步骤一样非常繁琐，难以记忆。那就还像上面一样沿着sample question的思路，一步一步运用到真题中。就这样不怕麻烦的“照猫画虎”，你就能更熟练的解题！
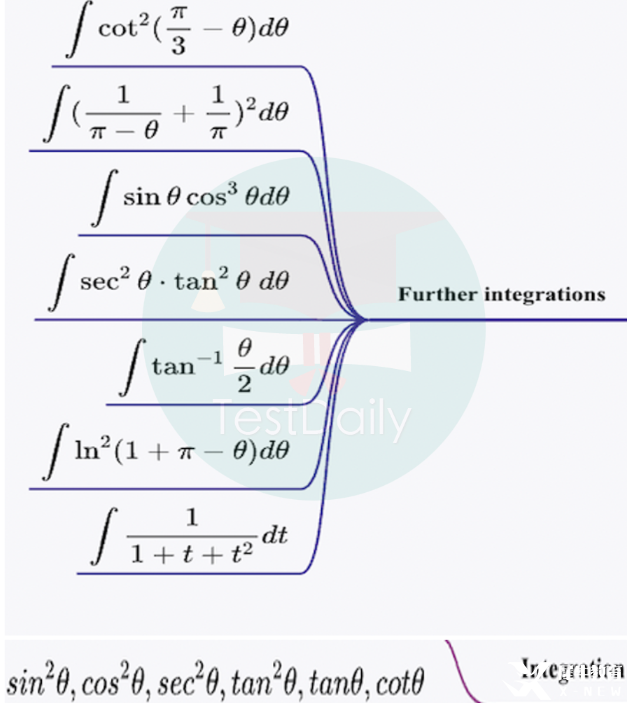
积分的计算真是太难算了！！同时他又遍布在所有的章节里面，FP1是要求我们掌握p3的各种积分方法的，所以你将会在polar算面积中收获一大堆复杂的积分运算。FP2则会系统的学习积分的很多种新方法，同样，在integration的章节中会大面积的考察。
积分还是强调熟练度和方法性，对于正在学FP1的同学，建议大家先学习p3的integration部分，并且按部就班的把书中的习题做完。同时可以养成总结积分的习惯，将paper中比较难或者常用的积分总结并记下来（就像这样），主打就是培养一个“眼熟”。正在学FP2的同学，inte是重灾区，建议秉持着能多练习就多练习的心态（刷完书本中的example，甚至去求解一些integration bee中的问题）。
图片为小编整理笔记
有些同学可能说FP和stats的大概学习方法和重难点已经明白了，那进阶力学肿么办？
mechanics相比于知识点的熟练掌握，还是更注重学生如何灵活的做题。就以FM的circular motion这个章节为例子，知识点就是向心力，向心加速度怎么算等，但是实际上你将会收获一堆有关string以奇奇怪怪的方法转的考题。所以学习并不是重点，勤于应用才是！
在每个章节结束之后，大家可以直接去past paper中找题刷，这里不光光要利用到“照猫画虎”的方法，也要懂得一个叫“ingredients”的方法。比如说以hookes law这章节为例子，我们可以如何描述一个string/spring/小球的运动呢，无非就是弹性系数，弹簧伸长量，弹簧上的受力，而他们都是互相可以用公式转化的。所以我们的老师也一直强调用已知求未知的方法一步步推进。先解决几个未知量，再挪向答案！
适合的才是最好的：
每个paper的重难点&应对策略
大概的学习步骤和方法就讲完了，下面来预告一下有什么难的章节和应对方法。
对于FP1来说，前三章都不算难，和pure的衔接还相对紧密。第一个难点出现在polar coordinates，知识点很少，但是area的部分需要大量的积分运算，如果是刚刚学完p1，那需要先补充integration的知识再去学习这部分。
第六章vector也是一个大考点（难点），基本的知识很简单，但是straight line和plane的方程如何求解，以及如何求解各种distance的问题还是很繁琐的。应对策略是用思维导图的方法理清楚考点，更重要的是，不要指望着能完全背下来distance公式，一定一定注重推导的过程。
第二章矩阵，可以算是一个难点，考试的时候出现的分数也很多。他的难点在于信息量特别特别大，并且基于FP1的矩阵做扩展。应对的方法是在学习FP2的矩阵之前抽时间复习FP1的内容，熟练的会算inverse，行列式和基础的计算。
学习的时候一定要用思维导图的形式进行整理，理清楚eigenvalue，eigenvector，diagonalisation，以及diagonalisation的拓展应用之间的关系。并且要不厌其烦地“照猫画虎”的刷题才能熟练掌握。
第四章integration，首先是加入了一大批新的integration并且要求我们熟练掌握像substitution这样的方法，熟练工比啥都重要！reduction formula是一个大大的难点，难点在于by parts分部积分不知道如何分才合理。这块需要我们懂得观察法，从需要求证的结果入手，反手推出如何合理的by parts。二话不说，咱们还是多做做题吧。
第六章de和matrix有异曲同工之妙，知识点超级多，并且还需要背诵second order的PI。应对策略还是思维导图和“照猫画虎”，学习的时候一定要理解particular integral（PI）和complementary function（CF）是什么，不然步骤背诵的有点像背天书。
Further Stats其实有点像“背书”。总之，题目中会给你一种场景，大家根据题目选定合适的hypothesis test。第二章节normal and t-distributions刚学习起来会有些理解上的困难，需要花时间去认识什么是hypothesis test以及背后的逻辑，但在“入门”之后学习别的检验方式就很轻松了！这部分建议大家在youtube上找一些normal distribution的视频（khan academy的系列很不错）
probability generating function将概率和函数进行结合，理解上也算是一个小难点。好在题目考察的方式统一，考刷题就够了。
further mechanics堪称是further math的计算天花板，很多的章节和al物理的syllabus重叠多，但是对定量计算要求更高。
第二章equilibrium of rigid body是一个大难点，我们需要算各种图形的center of mass（formula booklet里面有公式）此章节还涉及到toppling和moment的问题，这对我们受力分析的能力以及找合适的moment的能力要求较高，只能通过多刷题来提高熟练度。
第四章hooke’s law有些题目结合了energy和circular motion，考察比较综合。我认为这部分的知识难度不大，但是在做题的时候容易没有突破口，建议大家可以通过整理题型的方式瞄准每道题的考察点（到底是用energy做题呢，还是kinematic）总之，FM就是带着耐心刷题。
干货就讲到这啦。进阶数学的内容杂，的确需要同学们比较有耐心，踏踏实实的学习。虽然被称为“难度天花板”，但是希望大家看完这篇文章能更明确努力的方向。小小A*，速速拿下！
犀牛ALevel课程培训
犀牛国际现正火热招生中，专为暑假ALevel数学、ALevel物理、ALevel化学、ALevel生物和ALevel经济科目的大考设计了培优课程，旨在帮助学生们在考试中取得优异成绩。加入我们的课程，为即将到来的ALevel挑战做好准备吧！
-
课程类型：小班授课/一对一授课模式
-
授课模式：线上线下同步开课，可回放学习
-
授课语言：中英双语教学/纯英文授课
犀牛在北京、上海、广州、深圳、苏州、杭州、南京、无锡、青岛、成都、武汉、天津、合肥、宁波、重庆均开设线下校区，其他城市学员也可参加线上网课享受总部师资，欢迎咨询~
