A-Level基础数学纯数篇：一篇搞定P1/P2/P3考纲重难点、高频考点！

在A-Level考试中，数学一直是中国学生的优势科目，剑桥国际A-Level数学(9709)更是全球众多高校认可的“黄金标准”课程。

CAIEA-Level基础数学内容包含【纯数】、【力学】、【概率与统计】，注重深度与抽象思维，内容向大学数学延伸，考试要求逻辑推理与复杂问题解决能力。其中，纯数(Pure Mathematics)是A-Level数学的核心模块。

今天，老师就为大家带来一份超详细的【CAIE A-Level数学纯数模块学习指南】，带大家一览纯数P1. P2. P3详细考纲，锁定重难点与高频考点，并奉上独家学习建议，帮助同学们全面了解学习内容、把握考试重点、制定有效学习策略。

A-Level基础数学9709学什么？

在深入纯数之前，我们首先要对A-Level基础数学(9709)有一个宏观的认识。

CAIE A-Level数学(9709)考纲内容主要分为六大模块：

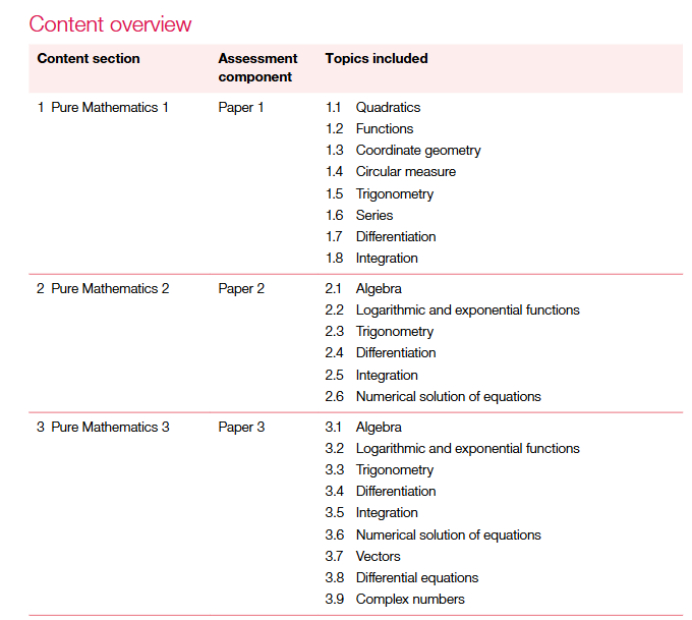
纯数1 (Pure Mathematics 1)

纯数2 (Pure Mathematics 2)

纯数3 (Pure Mathematics 3)

力学 (Mechanics)

概率与统计1 (Probability & Statistics 1)

概率与统计2 (Probability & Statistics 2)

这六大模块并非全部都要学习，考生需要根据自己报考的AS Level 还是A Level 以及所选的学习路径来选择相应的组合。

六大考试模块如何选择?

A-Level基础数学(9709)考试采用模块化考试形式，一共有6张paper，分为三大部分，各部分下又分为了不同的单元可供选择：

①纯数(Pure Math)：Paper1、Paper2、Paper3.涵盖了函数、几何坐标、三角学、微积分等核心数学内容。

②力学(Mechanics)：Paper4.主要探讨力与平衡、牛顿运动定律等力学原理。

③概率与统计(Probability & Statistics c) ：Paper5、Paper6. 包含S1、S2.涉及概率、统计推断等统计学基础知识。

AS Level(需考2张试卷)常见组合

P1 + P2(纯数路线，注意：此路线不能用于后续合成A-Level)

P1 + M(纯数+力学)

P1 + S1(纯数+统计)

A Level(需考4张试卷)常见组合

P1 + P3 + M + S1(最经典、最全面的组合)

P1 + P3 + S1 + S2(偏重统计方向的组合)

学生可以根据自己的兴趣和能力选择不同的模块进行考试。AS Level 数学考生需选修两个部分, A2考生需选修四个数学科目。每个模块都有独立的考试卷子和评分标准，最终成绩由多个模块的成绩综合而成。

从考试结构不难看出，无论选择哪种路径，Pure Mathematics 1 (P1) 是AS/A2考生的必选，而P3则是A Level阶段纯数的深化，要求更高。

纯数模块知识点梳理

模块一：纯数1

Pure Mathematics 1 (P1)

P1是所有学生的必选，无论是AS还是A-Level，它是整个AL数学课程的基础，其知识点会渗透到其他试卷中。

考试形式： 1小时50分钟，75分，10-12道结构化试题。

权重：占AS Level的60%，占A-Level的30%。

虽然P1内容相对基础，但概念理解至关重要，而且P1在考试中是关键的得分单元，所以一定要做到概念清晰、计算熟练，否则在这里模糊的知识点，都会在P3中被无限放大的。

核心知识点：

1.1Quadratics二次函数：配方法不仅要求过程，更要会用，例如，通过配方求抛物线顶点坐标，或草图绘制;学习判别式，必须熟练掌握因式分解、配方、求根公式三种方法，并能根据题目选择最简捷的一种;解二次方程与不等式、解可化为二次型的方程，这是难点。

重难点：配方法求顶点位置，判别式判断根的情况，需要理解“重根”的概念;解含参数的二次方程。

1.2 Functions函数：理解函数、定义域、值域、一一函数、反函数、复合函数的概念;求给定函数的值域(简单情况)，以及两个函数的复合函数;判断给定函数是否为一对一函数，并求一对一函数的反函数(简单情况)，用图形说明一一函数与其反函数的关系;理解并使用函数图像的变换(平移、伸缩、反射)。

重难点：函数变换，值域、定义域的求法，对复合变换的理解和图像绘制，特别是反函数(别忘记定义域)比较难，反函数难点在于限制定义域使其成为一一函数。

1.3 Coordinate geometry坐标几何：直线方程的各种形式，根据给定信息求直线方程，圆的方程(标准式和一般式)，直线与圆的位置关系，理解图形与其对应方程的关系，并利用图形交点与方程解的关系。

重难点：直线方程，计算包括距离、斜率、中点、交点，以及平行和垂直直线的斜率关系;圆的方程;几何性质，会运用圆的切线垂直于半径、半圆上的圆周角是直角、对称性等基本几何性质，不包含隐函数求导;理解图形与方程的对应关系。

1.4 Circular measure弧度制：理解弧度的定义，以及弧度与度的关系，使用公式决涉及弧长和扇形面积的问题。

重难点：弧度制下的三角函数计算。

1.5 Trigonometry三角函数：绘制和使用sin, cos, tan的图像与性质，特殊角三角函数值，理解反函数的概念，使用符号表示反三角函数主值，基本三角恒等式，求在指定区间内的简单三角方程的所有解(不要求通解的一般形式)。

重难点：三角恒等式的证明和应用，解复杂三角函数方程。

1.6 Series数列：二项式展开，等差数列与等比数列的通项与求和公式，使用等比数列的收敛条件，以及收敛等比数列的无穷项和公式，等比数列的无穷项求和。

重难点：二项式定理的应用，数列求和技巧，应用题题目可能涉及多个数列。

1.7微分Differentiation：微分的概念与记号;幂函数、复合函数的求导;应用(切线法线、单调性、极值点)。

重难点：极限概念，从极限角度理解导数，复合函数求导，应用问题建模。

1.8 积分Integration：积分作为微分的逆运算，幂函数、简单复合函数的积分;不定积分、定积分，定积分求面积和旋转体体积。

重难点：理解积分概念，对导数作为“极限”的直观理解，以及利用积分求旋转体体积(特别是绕y轴旋转或非封闭区域旋转)。

P1高频考点：

利用判别式判断根的情况。

函数图像变换(平移、伸缩、反射)，求函数的反函数并说明其定义域。

圆的几何性质与代数方程的结合(如切线问题)，直线与圆的位置关系。

弧长和扇形面积的计算。

利用恒等式简化表达式，解特定区间内的三角方程。

等差数列和等比数列的判定与求和。

利用微分求切线方程，判断函数单调性，求函数的极值点并判断其性质。

利用定积分求曲线与坐标轴或另一条曲线所围成的面积。

模块二：纯数2

Pure Mathematics 2 (P2)

纯数P2在纯数1的基础上深化和扩展，引入了更多高级概念，知识点与P1和P3有大量重叠。仅作为AS Level的一部分。选择仅考AS Level的学生，可与P1组合。注意： P1+P2这条纯数路线不能计入A-Level成绩。

考试形式： 1小时15分钟，50分，6-8道结构化试题。

权重：占AS Level的40%。

核心知识点：

2.1 Algebra代数：绝对值函数与方程/不等式;多项式除法;使用因式定理与余数定理。

重难点：解含绝对值的方程和不等式，多项式除法，用于求因式和余式，解多项式方程或求未知系数。

2.2 Logarithmic and exponential functions对数和指数函数：对数定律，理解对数与指数的关系，并使用对数法则(不包括换底公式);理解e^x 和 ln x 的定义、性质，包括它们作为反函数的关系及其图像;使用对数解未知数出现在指数中的方程和不等式;将非线性关系化为线性形式。

重难点：理解自然对数和指数函数作为反函数的关系。

2.3 Trigonometry三角函数：理解正割、余割、余切函数与余弦、正弦、正切函数的的定义、图像与性质;使用三角恒等式简化和精确求值表达式，以及在解方程过程中使用，能根据情境选择合适的恒等式。

重难点：复杂的三角恒等式证明与化简及应用，特别是 a sinθ + b cosθ 的合成。

2.4 Differentiation微分：指数、对数、三角函数的导数;乘积法则与商法则;参数方程与隐函数求导(一阶)。

重难点：隐函数求导及其在求切线方程中的应用。

2.5 Integration积分：指数、对数、三角函数的积分;利用三角恒等式积分;理解并使用梯形法则估算定积分的值。

重难点：利用三角恒等式简化被积函数。梯形法则，包括在简单情况下使用草图判断梯形法给出的是过高估计还是过低估计。

2.6 Numerical solution of equations方程的数值解法：通过图像法或符号法定位根;理解收敛于方程根的近似序列的概念并使用其符号，理解给定的简单迭代公式求根。

重难点：定位根，例如，找出一对连续整数，使得根位于它们之间。理解迭代过程的收敛性。

P2的三角函数和微积分难度显著提升，需要大量练习来巩固技巧，迭代法部分理解其思想即可，计算通常不复杂。

高频考点：

利用因式定理/余数定理求多项式未知系数。

利用线性化方法确定未知常数，解涉及 e^x 和 ln x 的方程。

将asinθ+bcosθ化为Rsin(θ±α)或Rcos(θ±α)形式

使用乘积法则/商法则进行微分。

利用对数将 y = kx^n 或 y = k a^x 线性化，并通过图表信息确定常数。

模块三：纯数3

Pure Mathematics 3 (P3)

P3是A-Level纯数的核心，在P1、P2基础上新增和深化， A-Level学生的必修模块，是纯数内容的最高阶，也是大学数学的预备课程，难度最大，内容最深，是冲击A*的关键。

考试形式： 1小时50分钟，75分，9-11道结构化试题。

权重： 占A-Level的30%。

P1 涵盖的微积分、三角函数、函数等基础内容，在P3难度明显升级。与纯数P1相比，P3不仅增加了更多抽象和高阶的概念，还对学生的数学分析能力进行了提升，所以P3一向是公认的最头疼甚至“挂科”的重灾区。

举例：

积分方法大幅增加，除了基础积分公式外，像分部积分、换元积分、分式积分等都要学。

三角应用也更复杂，比如会用到R-formula。

函数方面讨论更深入，涉及到绝对值函数、对数指数函数等复杂类型。

核心知识点：

3.1 Algebra代数：理解绝对值，绘制图像，解方程和不等式;多项式除法、因式定理和余数定理;回忆有理函数部分分式的合适形式，并进行分解、二项式展开。

重难点：部分分式分解，有理指数二项式展开。

3.2 Logarithmic and exponential functions对数和指数函数 & 3.3 Trigonometry三角函数：内容与P2高度重合，但考核的深度和综合度更高。

重难点：复杂情境下的应用。

3.4 Differentiation微分：指数、对数、三角函数及反三角函数的导数、乘积法则和商法则、参数方程和隐函数求导。

重难点：反三角函数求导，复杂隐函数求导。

3.5 Integration积分：各类函数积分、三角恒等式在积分中的应用、通过分解为部分分式积分有理函数、换元积分法、分部积分法。

重难点：积分技巧的综合运用：尤其是根据被积函数形式，灵活选择分部积分法或代换法，这是P3最大的难点。

3.6 Numerical solution of equations方程的数值解法：与P2内容基本相同，但要求更高。

重难点：复杂方程的数值解法。

3.7 Vectors向量：使用向量的标准符号，进行向量的加、减和标量乘法，并从几何角度解释这些运算;计算向量的大小，并使用单位向量、位移向量和位置向量;理解直线方程，并根据给定信息求直线方程;向量位置关系;使用公式计算两个向量的数量积，并在涉及直线和点的问题中使用数量积。

重难点：向量是IG和A-Level数学都会涉及到的知识点，也是一大难点。A-Level的向量部分难度显著提升，引入更复杂的运算，如向量的分解、三维空间中的向量、向量在力学和物理中的应用，以及更深入的几何和代数应用，尤其是空间向量 (Vectors in 3D)，强调抽象思维与跨学科应用，理解起来很难，需要额外学习三维向量的模长、方向角及点积/叉积的几何意义，并结合力学(如力的分解、动量守恒)和物理问题，提升向量在复杂场景中的建模能力。

3.8 Differential equations微分方程：将涉及变化率的简单陈述表述为微分方程，通过积分求一阶可分离变量微分方程的通解，使用初始条件求特解，在微分方程所建模的问题背景下解释解。

重难点：建立并求解可分离变量的微分方程;利用初始条件求特解，建模。

3.9 复数：理解复数概念和运算、共轭复数、模和辐角、复数的几何表示、复数极坐标形式、复数开方。

重难点：复数的几何意义，在阿贡图上表示 |z - a| = k， arg(z - a) = θ 等轨迹，复数极坐标形式的乘除运算，复数方程和不等式的几何表示。

P3的重点是积分和复数。微积分是A-level数学的重要关键内容。相比之下，微分要简单些，主要就是基本求导公式、和差积商求导法则以及链式法则等技巧。积分就不一样了，除了基本积分公式外，还涵盖诸多技巧，像逆链式法则、换元积分、三角恒等式、部分分式以及分部积分等。

在积分问题里，三角函数积分又是重点+难点，它既涉及三角恒等关系式，又会用到积分技巧，不少学生对这块内容特别犯怵，一遇到这类题目就觉得十分棘手。

积分没有捷径，唯有多练。赛思老师已经把【纯数里面的积分以及和三角函数相关的积分高频题】都整理好了，而且IB的学生也能拿去练练手。复数则要打通代数形式和几何意义的关联，理解其作为“二维数”的本质。